
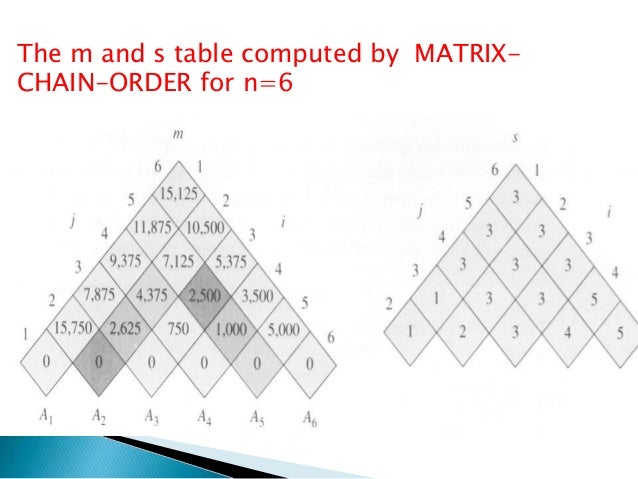
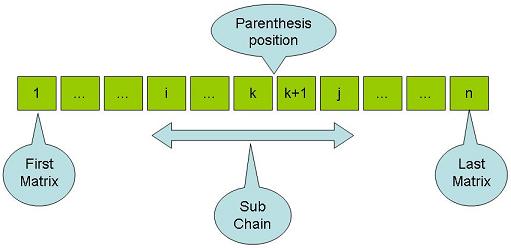
The minimum number of multiplications among all the first partitions is the required answer.įollow the steps mentioned below to implement the approach:.Each of the groups can be further partitioned into smaller groups and we can find the total required multiplications by solving for each of the groups.

So a range can be broken into two groups like. For example, sequence of matrices A, B, C and D can be grouped as (A)(BCD), (AB)(CD) or (ABC)(D) in these 3 ways. Now, for a given chain of N matrices, the first partition can be done in N-1 ways. Dynamic Programming | Wildcard Pattern Matching | Linear Time and Constant Space.Find minimum sum such that one of every three consecutive elements is taken.Find the longest path in a matrix with given constraints.Find if string is K-Palindrome or not | Set 1.Minimum number of deletions to make a string palindrome.Maximum number of trailing zeros in the product of the subsets of size k.Maximum subarray sum in O(n) using prefix sum.Count number of ways to partition a set into k subsets.Count number of ways to jump to reach end.Find all distinct subset (or subsequence) sums of an array.Longest Palindromic Subsequence | DP-12.Travelling Salesman Problem using Dynamic Programming.Intermediate problems of Dynamic programming ISRO CS Syllabus for Scientist/Engineer Exam.ISRO CS Original Papers and Official Keys.GATE CS Original Papers and Official Keys.Full Stack Development with React & Node JS(Live).Java Programming - Beginner to Advanced.OS DBMS CN for SDE Interview Preparation.Data Structure & Algorithm-Self Paced(C++/JAVA).

Input: Output: Objective: a chain of matrices to be multiplied a parenthesizing of the chain minimize number of steps needed for the multiplication Matrix multiplication: A of size m x n, B of size n x p How many steps to compute A.B ? Input: Output: Objective: a chain of matrices to be multiplied a parenthesizing of the chain minimize number of steps needed for the multiplication


 0 kommentar(er)
0 kommentar(er)
